Преобразование внутренних сил для перемещения замкнутой системы

Берников В.Р., Преобразование внутренних сил для перемещения замкнутой системы., «Актуальные проблемы современной науки», № 3(120), 2021 г., ISSN 1680-2721, стр.46-55

Энергия вращательного движения может переходить в энергию поступательного движения и наоборот [3, с.424-428], доказано на примере взаимодействия двух стержней с шарами на концах. Кроме того, приведено математическое доказательство и экспериментальное подтверждение [4, с.28-41] движения центра масс под действием внутренних сил на примере полого и сплошного цилиндров одинакового внешнего диаметра и равной массы при движении по наклонной поверхности. А также приведено математическое доказательство с выводом уравнений движения центра масс [5, с.197-202] на примере двух грузов, вращающихся синхронно навстречу друг другу, то есть импульс центра масс системы может быть изменён путём изменения внутреннего вращательного импульса или внутреннего поступательного импульса. Существует математическое доказательство [6, с.139-142] движения центра масс системы тел под действием внутренних сил для замкнутой системы с колечками на стержне, взаимодействующих с ускорением под действием пружин, и выведено уравнение движения центра масс под действием внутренних сил.

Рассмотрим основные теоремы классической механики для поступательного движения и их условия применения.

Теорема о движении центра масс [1, с.44-45]: центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к точкам системы.

M(dv_C/dt) = ∑ F^e (1.1)

Теорема об изменении количества движения [1, с.49-50]: производная по времени от количества движения механической системы равна главному вектору всех внешних сил.

d(mv)/dt = ∑ F^e (1.2)

Следует отметить, что теорема об изменении количества движения тождественна теореме о движении центра масс [1, с.54] и, кроме того, теорема о движении центра масс [2, с.290] является следствием теоремы об изменении количества движения.

Следствием из теоремы об изменении количества движения системы является закон сохранения количества движения [1, с.50]: если главный вектор внешних сил равен нулю, то количество движения системы остаётся постоянным.

mv = const (1.3)

Равенства (1.1), (1.2), (1.3) верны для прямолинейного движения при условии, что сумма внутренних сил равна нулю ∑Fⁱ= 0.

Теорема об изменении кинетической энергии системы тел [1, с.78-80]: изменение кинетической энергии при переходе механической системы из одного положения в другое равно сумме полных работ всех внешних и внутренних сил.

Т₂ — Т₁ = ∑А^e +∑Аⁱ (1.4)

Равенство (1.4) верно для прямолинейного, вращательного и сложного движения.

Главное отличие теоремы об изменении кинетической энергии от выше названных заключается в том, что она выполняется для всех видов движения и кинетическая энергия зависит от работы внутренних сил.

Окончательно, можно составить таблицу условий выполнения основных теорем механики поступательного движения для замкнутой (∑F^e= 0, ∑А^e = 0, ∑Аⁱ ≠ 0) системы тел, которые отображены в таблице 1.

Таблица 1

Рассмотрим выполнение закона сохранения импульса (количества движения) в замкнутой системе тел в общем случае для сложного движения.

1 Работа внутренних сил (∑Аⁱ = 0) равна нулю.

Пусть система состоит из двух движущихся прямолинейно навстречу друг другу тел массой m₁ и m₂ со скоростью v₁ и v₂ соответственно. После абсолютно упругого взаимодействия тела приобретают в первом случае прямолинейное движение со скоростями v₃ и v₄, а во втором случае сложное движение: прямолинейное движение со скоростями v₅ и v₆ и вращательное с угловыми скоростями w₁ и w₂ соответственно. Отметим, что при абсолютно упругом взаимодействии работа внутренних сил (∑Аⁱ = 0) равна нулю.

Запишем закон сохранения импульса и кинетическую энергию до и после взаимодействия для первого случая

m₁v₁ + m₂v₂ = m₁v₃ + m₂v₄ = C₁ (1.5)

m₁(v₁)²/2 + m₂(v₂)²/2 = m₁(v₃)²/2 + m₂(v₄)²/2. (1.6)

Легко доказать, что система уравнений из формул (1.5) и (1.6) имеет решение, то есть закон сохранения импульса выполняется.

Запишем кинетическую энергию для второго случая

m₁(v₁)²/2 + m₂(v₂)²/2 = m₁(v₅)²/2 + m₂(v₆)²/2 + J₁(w₁)²/2 + J₂(w₂)²/2. (1.7)

При ближайшем рассмотрении формул (1.6) и (1.7), очевидно, что кинетическая энергия прямолинейного движения после взаимодействия во втором случае меньше и, при сохранении одинаковой направленности скоростей, величина скорости тоже меньше, то есть

v₅ < v₃ (1.8)

и

v₆ < v₄. (1.9)

Запишем сумму импульсов для второго случая до взаимодействия, учитывая формулу (1.5)

m₁v₁ + m₂v₂ = C₁. (1.10)

Теперь запишем сумму импульсов для второго и первого случая после взаимодействия

m₁v₅ + m₂v₆ = C₂ (1.11)

m₁v₃ + m₂v₄ = C₁. (1.12)

Учитывая неравенства (1.8) и (1.9), очевидно, что

C₂ < C₁. (1.13)

Значит во втором случае сумма импульсов прямолинейного движения до взаимодействия и после взаимодействия не равны друг другу

m₁v₅ + m₂v₆ < m₁v₁ + m₂v₂. (1.14)

Таким образом, закон сохранения импульса для второго случая сложного движения с прямолинейным и вращательным движением в данном случае при работе внутренних сил равной нулю не выполняется.

Следовательно, при сложном движении центр масс замкнутой системы тел меняет своё положение

2 Работа внутренних сил (∑Аⁱ ≠ 0) не равна нулю.

Пусть система состоит из двух тел массой m₁ и m₂, в начальный момент времени находящихся в покое. После абсолютно упругого взаимодействия тела приобретают в первом случае прямолинейное движение со скоростями v₁ и v₂, а во втором случае сложное движение: прямолинейное движение со скоростью v₃ и угловой скоростью w₁ для первого тела и, очевидно, той же, как в первом случае, прямолинейной скоростью v₂ для второго тела.

Запишем закон сохранения импульса и кинетическую энергию после взаимодействия для первого случая

m₁v₁ + m₂v₂ = 0 (1.15)

m₁(v₁)²/2 + m₂(v₂)²/2 = А₁+А₂. (1.16)

Легко доказать, что система уравнений из формул (1.15) и (1.16) имеет решение, то есть закон сохранения импульса выполняется.

Запишем кинетическую энергию для второго случая

m₁(v₃)²/2 + J₁(w₁)²/2 + m₂(v₂)²/2 = А₁ +А₂ (1.17)

При ближайшем рассмотрении формул (1.16) и (1.17), очевидно, что кинетическая энергия прямолинейного движения тела массой m₁ после взаимодействия во втором случае меньше, а значит и скорость тоже меньше, то есть

v₃ < v₁. (1.18)

Запишем закон сохранения импульса для второго случая после взаимодействия

m₁v₃ + m₂v₂ = 0. (1.19)

Из формул (1.15) и (1.19) найдём скорости v₁и v₃ получим

v₁ = -m₂v₂ /m₁ (1.20)

v₃ = -m₂v₂ / m₁. (1.21)

Из формул (1.20) и (1.21) вытекает, что v₃ = v₁, но согласно доказанному по формуле (1.18) v₃ < v₁. Получили противоречие. Следовательно, закон сохранения импульса не выполняется и в этом случае, то есть при работе внутренних сил не равной нулю и сложном движении центр масс замкнутой системы тел, находящийся в начальный момент времени в покое, меняет своё положение.

Таким образом, при взаимодействии тел со сложным движением центр масс замкнутой системы меняет своё положение.

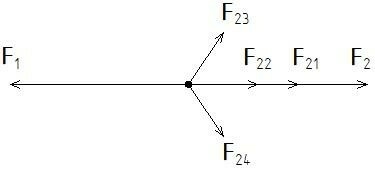
Тогда, например, при взаимодействии двух тел можно сделать вывод, что возникают симметричные (рис 1) противоположно направленные равные силы F₂₃ и F₂₄, вызывающие вращение, но при этом сумма всех внутренних сил равна нулю. То есть, согласно 3-му закону Ньютона силы, действующие при взаимодействии двух тел равны и противоположно направлены F₁ = -F₂. Так как второе тело начинает вращаться и двигаться поступательно, тогда вектор

F₂ = F₂₁ + F₂₂, (1.22)

где F₂₁ — вектор силы поступательного движения,

F₂₂ — вектор силы вращательного движения.

Вектор силы вращательного движения равен по правилу параллелограмма

F₂₂ = F₂₃ + F₂₄. (1.23)

 © Фото из открытых источников

Рис 1

Следовательно, в замкнутой системе тел при их взаимодействии со сложным движением возникают внутренние силы оказывающие разное влияние на характер движения тел, что позволяет силы, вызывающие вращение, не учитывать для поступательного движения и выделить силы — динамические силы, которые обеспечивают поступательное движение и, которые должны фигурировать в теореме об изменении количества движения, как другой вид внутренних сил.

Динамической силой в данном примере является разность между абсолютными значениями силы взаимодействия 1-го тела F₁ и силы взаимодействия поступательного движения 2-го тела F₂₁

F^id = F₁ — F₂₁ (1.24)

Таким образом, теорема об изменении количества движения должна формулироваться следующим образом: производная по времени от количества движения механической системы равна главному вектору всех внешних и внутренних динамических сил.

d(mv)/dt = ∑ F^e +∑F^id (1.25)

Соответственно изменится и закон сохранения количества движения: если главный вектор внешних и внутренних динамических сил равен нулю, то количество движения системы остаётся постоянным.

mv = const (1.26)

Теорема о движении центра масс так же изменится: центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная геометрической сумме всех внешних и внутренних динамических сил, приложенных к точкам системы.

M(dv_C /dt) = ∑ F^e +∑F^id (1.27)

Теперь можно составить таблицу условий выполнения основных теорем механики поступательного движения для замкнутой (∑F^e= 0, ∑F^id = 0, ∑F^id ≠ 0, ∑А^e = 0, ∑Аⁱ ≠ 0) системы тел, которые отображены в таблице 2.

Таблица 2

Вывод: безопорное поступательное движение для замкнутой системы тел- это движение под воздействием внутренних динамических сил, возникающих при преобразовании прямолинейного импульса одного из взаимодействующих тел во вращательное или колебательное.

Литература.

1. Андронов В.В. Теоретическая механика. 20 лекций. Ч.2. Динамика: Учебное пособие для студентов очного и заочного обучения. Спец. 260100 и 260200. 2-е изд., доп. и испр. — М.: МГУЛ, 2003, — 128 с.
2. Добронравов В.В., Никитин Н.Н. Курс теоретической механики: Учебник для машиностроит. спец. вузов. — 4-е изд., перераб. и доп. —М.: Высш. школа", 1983, — 575 с., ил.
3. Хайкин С.Э. Физические основы механики, М.: Наука, 1971, 752с.
4. Турышев М.В., О движении замкнутых систем, или при каких условиях не выполняется закон сохранения импульса., «Естественные и технические науки»,№ 3(29), 2007, ISSN 1684-2626.
5. Шипов Г. И. Теория физического вакуума. Теория эксперименты и технологии. 2-е изд., — М.:Наука, 1996, 456с
6. Геронимус Я. Л. Теоретическая механика (очерки об основных положениях): Главная редакция физико-математической литературы изд-ва «Наука», 1973 г., 512с.) .

Кстати, а вы знали, что на «Сделано у нас» статьи публикуют посетители, такие же как и вы? И никакой премодерации, согласований и разрешений! Любой может добавить новость. А лучшие попадут в телеграмм @sdelanounas_ru. Подробнее о том как работает наш сайт здесь👈