Что нам стоит свет построить… (открывая тайны голограммы)

Ученым из Самарского филиала (СФ) Физического института им. П.Н. Лебедева РАН удалось теоретически описать распространение структурно устойчивых когерентных световых пучков и их преобразование в линейных оптических системах. Результаты этих исследований открывают возможность создания лазеров, генерирующих пучки с заданными свойствами, что важно для развития лазерной оптики, медицины, технологии обработки металлов. О результатах исследований «ФИАН-информ» рассказала сотрудник лазерно-измерительной лаборатории СФ ФИАН Евгения Вадимовна Разуева.

• 
• raz4

_{На рисунке: Спиральный пучок сложной структуры (интенсивность и фаза). Несмотря на свой «рукотворный» вид, данный пучок такой же естественный физико-математический объект, как и обычные лазерные пучки, является точным решением уравнения Шредингера и сохраняет структуру интенсивности при распространении}

Как известно, распространение светового поля, в частности лазерного пучка, представляет собой волновое явление и описывается распределением интенсивности и фазы в поперечном сечении. При распространении световое поле, вообще говоря, претерпевает количественные и качественные изменения.

Однако несколько иначе обстоит дело с когерентным излучением. С открытием лазеров и развитием когерентной оптики появились экспериментальные и теоретические работы, доказывающие существование пучков когерентного света, сохраняющих структуру интенсивности в поперечном сечении при распространении и фокусировке с точностью до масштаба. Эти пучки называются модами когерентного излучения и являются собственными колебаниями лазерных резонаторов. Они имеют жестко заданную форму и описываются двумя семействами специальных функций с различными типами симметрии: моды Эрмита-Гаусса и моды Лагерра-Гаусса. Простейшим представителем обоих семейств является хорошо известный гауссов пучок.

Моды Эрмита-Лагерра-Гаусса

«Существование пучков Эрмита-Гаусса и Лагерра-Гаусса экспериментально было доказано еще в 60-х годах. Долгое время считалось, что эти пучки являются двумя независимыми семействами, обладающими структурной устойчивостью и различающимися между собой симметрией. Однако позднее было теоретически доказано и показано экспериментально, что при задании определенных параметров оптической системы возможно преобразование одного типа пучка в другой. Более того, удалось определить новое семейство пучков — моды Эрмита-Лагерра-Гаусса, — которое включает в себя все моды Эрмита-Гаусса и Лагерра-Гаусса и позволяет аналитически описать все возможные преобразования этих мод в линейных оптических системах. Было показано, что в любой линейной оптической системе пучок Эрмита-Лагерра-Гаусса преобразуется в пучок Эрмита-Лагерра-Гаусса с другими параметрами. Таким образом, преобразование светового пучка полностью определяется преобразованием параметров пучка. Оказалось, что преобразование мод Эрмита-Лагерра-Гаусса в линейных оптических системах можно рассматривать как вращения в трехмерном пространстве» — рассказывает Евгения Вадимовна.

Этот результат, потребовавший долгой и весьма кропотливой работы, имеет огромное значение для когерентной оптики: имея описание преобразования одних пучков в другие, зная параметры входного излучения и желаемые параметры выходного, можно определить необходимые параметры оптической системы. В результате такой работы появилась возможность создания лазеров, которые без дополнительной нестандартной оптики смогут генерировать излучение с требуемыми характеристиками. Фактически, исследователям из СФ ФИАН удалось решить одну из множества задач по развитию методов управления характеристиками световых пучков, возникающих в лазерном резонаторе.

Спиральные пучки

Оказывается, понятие структурной устойчивости световых полей можно расширить и рассмотреть вопрос существования таких лазерных пучков, которые сохраняют структуру интенсивности при распространении и фокусировке с точностью до масштаба и вращения.

В СФ ФИАН был найден целый класс лазерных пучков, названных спиральными, которые сохраняют свою структуру при распространении и фокусировке и могут иметь различные параметры вращения. Упомянутые выше пучки Эрмита-Гаусса, Лагерра-Гаусса и Эрмита-Лагерра-Гаусса являются частными случаями таких спиральных пучков (отсутствие вращения — это нулевое вращение).

• 
• raz3

_{На рисунке: Примеры спиральных пучков в виде плоских кривых (верхний ряд — интенсивности, нижний ряд — фазы). Красными кружочками выделены дислокации волнового фронта, или оптические вихри — точки поля, в которых амплитуда излучения равна 0, а фаза неопределенна}

Семейство спиральных пучков оказалось достаточно широким. В частности, можно построить спиральные пучки, распределение интенсивности которых имеет форму произвольной плоской кривой или их совокупности. В отличие от световых полей с заданным распределением интенсивности, формируемых известными ранее методами, эти спиральные пучки сохраняют свою структуру в любой плоскости наблюдения и фокусировки. Таким образом, данное свойство спиральных пучков позволяет весьма гибко менять их форму при сохранении структурной устойчивости. Это может представлять интерес для лазерной медицины и технологии.

Спиральные пучки являются вихревыми полями. Исследования вихревых световых полей, получивших свое развитие в совершенно новом для лазерной физики направлении «сингулярной оптики», являются одним из самых последних и бурно развивающихся направлений исследований.

Характерными особенностями вихревых полей является наличие особых точек волнового фронта — дислокаций или оптических вихрей, в которых значение амплитуды равно 0, а фаза неопределенна. В природе возникновение вихревых световых полей во многом обусловлено неоднородностями среды, в которой происходит распространение светового пучка. Однако у физиков наибольший интерес вызывает случай генерирования световых вихрей с заданными параметрами в лазерных резонаторах.

Спиральные пучки обладают существенно ненулевым угловым моментом количества движения. Это проявляется в том, что микроскопические объекты размерами в десятки микрон (например, живые клетки), помещенные в область фокусировки такого пучка могут приводиться во вращение вокруг своего центра инерции, удерживаться в заданной области пространства, подвергаться неоднородным заданным деформациям и т. п.

На основе теории спиральных пучков могут быть построены фазовые элементы для фокусировки лазерного излучения с высокой эффективностью (разработан численный алгоритм). Сформированные таким образом поля также являются вихревыми и обладают угловым моментом.

Эти свойства дают возможность создания в области фокусировки заданных микрораспределений интенсивности и углового момента, что представляет удобный инструмент для бесконтактного манипулирования микрообъектами в электронике и микробиологии.

Экспериментальная реализация спиральных пучков может осуществляться различными методами. Во-первых, непосредственно с помощью амплитудно-фазовых масок. Другой, менее очевидный метод синтеза таких пучков, основан на обобщении преобразования пучков Лагерра-Гаусса в пучки Эрмита-Гаусса и сводится к синтезу одномерного по структуре поля («штрих-код»), которое преобразуется в оптической системе, состоящей из набора цилиндрических линз.

Исследования спиральных пучков показали, что они являются собственными колебаниями специфических резонаторов с вращением поля (был реализован аргоновый лазер с таким резонатором). Это показывает принципиальную возможность создания лазеров, непосредственным результатом генерации которых без дополнительной нестандартной оптики будут пучки с заданными свойствами.

Результаты, полученные самарскими физиками, имеют большое значение для развития сингулярной оптики. В настоящее время вихревые световые поля широко используются в лазерных технологиях обработки материалов, благодаря обеспечению более равномерного распределения температуры. А возможность сохранения структуры в любой плоскости распространения и фокусировки, а также ненулевой угловой момент количества движения позволяют предложить эти поля как весьма перспективный инструмент бесконтактного манипулирования микрообъектами, например, в микробиологии или электронике.

• 
• raz5

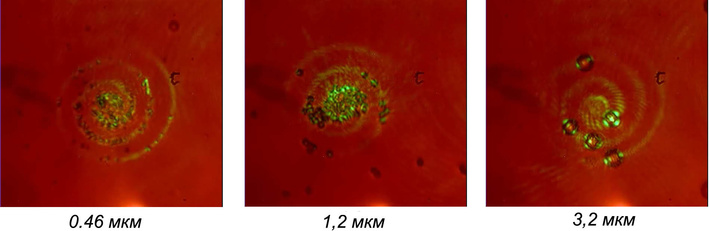
_{На рисунке: Экспериментальная реализация спиральных пучков: перемещение частиц латекса различных размеров вдоль заданной кривой}

Отдельно следует отметить, что теоретические и экспериментальные работы в области физики когерентных световых полей, в т. ч. и вихревых, дали толчок к развитию новых исследований полей совершенно иной физической природы: акустических, радиоволн и многое другое. Работы ученых из Самарского филиала ФИАН играют в этих исследованиях одну из ключевых ролей. Можно сказать, что российские физики создали новую технологию «конструирования» излучения, способную придавать ему весьма причудливые формы.

Е. Любченко, АНИ «ФИАН-информ»

_________________________________________

^{P. S. Все фото- и видеоматериалы предоставлены Е.В. Разуевой}

Кстати, а вы знали, что на «Сделано у нас» статьи публикуют посетители, такие же как и вы? И никакой премодерации, согласований и разрешений! Любой может добавить новость. А лучшие попадут в телеграмм @sdelanounas_ru. Подробнее о том как работает наш сайт здесь👈